红黑树详解

本文摘抄自浅谈红黑树 - bf 的博客，修改了叙述语言，并重绘了所有示意图

概念讲解

红黑树是一棵树（雾

红黑树的性质

节点为红色或黑色
NIL 节点（空叶子节点）为黑色
红色节点的子节点为黑色（注意黑色节点的子节点依然可以为黑色）
从根节点到 NIL 节点的每条路径上的黑色节点数量相同
引理 4.1 根节点为黑色

为了方便，下文中将从根节点到 NIL 节点的每条路径上的黑色节点数量称为黑高度

红黑树

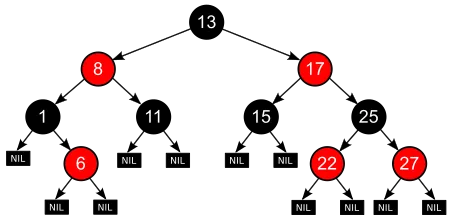
我们先定义一下节点，然后定义几个宏用来辅助计算

#define fa(x) (rbt[x].fa)
#define siz(x) (rbt[x].siz)
#define cnt(x) (rbt[x].cnt)
#define v(x) (rbt[x].v)
#define color(x) (rbt[x].color)
struct node{
    bool color; // 1->red 0->black
    int ch[2];
    int cnt;
    int fa;
    int siz;
    int v;
};

旋转

我们知道，如果数据很差（比如顺序排列）的情况下，树会退化成链，性能会大大降低，因此我们要调整平衡，让树不那么偏。而调整平衡的方式，就叫做旋转。不仅是红黑树有旋转，Splay/AVL也有（Treap：呜呜呜你们不带我玩）。

iwq5njyv.bpz-modified.png

以左旋为例，我们要做的是就是将 L 的右孩子设为 R 的左孩子，L 的父亲的孩子设为 R，R 的左孩子设为 L

void update_siz(int cur){
    siz(cur)=siz(rbt[cur].ch[0])+siz(rbt[cur].ch[1])+cnt(cur);
}
void rotate(int cur,bool dir){ // left 0 right 1
    int c1=rbt[cur].ch[!dir]; // 获取 R
    rbt[cur].ch[!dir]=rbt[c1].ch[dir]; // L 的右孩子设为 R 的左孩子 
    if(rbt[c1].ch[dir]) fa(rbt[c1].ch[dir])=cur; // 如果 R 的左孩子存在，则设置父亲为 L
    fa(c1)=fa(cur); // R 的父亲为 L 的父亲
    if(!fa(cur)){ // L 的父亲的孩子设为 R（考虑 L 的父亲为根）
        rt=c1;
    }else{
        rbt[fa(cur)].ch[isch(cur)]=c1;
    }
    rbt[c1].ch[dir]=cur; // R 的左孩子设为 L
    fa(cur)=c1; // L 的父亲设为 R
    update_siz(cur); 
    update_siz(c1);
}

插入

查找

就按照普通的平衡树操作鸭，但是要记录下父亲以便插入
最好的状况就是插入的数据在树里已经存在了，我们只需要将 cnt++ 就行了
顺便我们可以给每个遍历过的节点 siz 都 ++，因为这些都是新插入节点的父亲

维护

当我们插入新节点之后，一个问题就随之而来了：该赋予什么颜色呢？

如果插入之前没有节点，那插入的就是根，根据引理 4.1，给个黑色就完事了。
如果插入的不是根节点，那么首先考虑父节点
- 如果父节点为黑色，为了不违背性质 4，我们给个红色，这样不会影响黑高度
- 如果父节点为红色，那么就大事不得了了，根据性质 2，我们无论如何也会影响黑高度
  既然改变不了自己，那就
  
  ~~那我就，把这个幻想完全粉碎~~
  
  咳咳，也就是说我们要更改其他结构来平衡黑高度
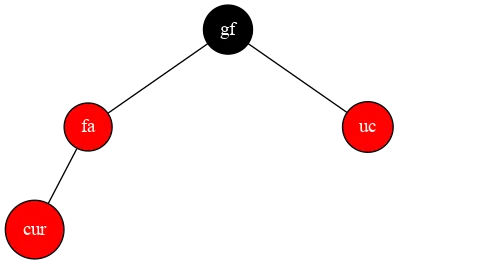
  在平衡时，我们遵循一个原则，如果能在本层解决，就在本层解决
  
  情况1：祖父的另一个孩子为黑色
  
  为了方便起见，我们将第二张图绕 fa 左旋，得到了如下图所示的样子。我们交换 fa，cur 以便后续操作。
  ⇒
  对于这种情况来说，我们只需要绕 gf 右旋，将 fa 设为黑色，gf 和 cur 设为红色
  
  情况2：祖父的另一个孩子为红色
  
  这种情况下我们能做的就是将祖父的另一个孩子设为黑色来使局部黑高度平衡。但是整体的黑高度多了 1
  于是我们将祖父设为红色。但这样又有可能与祖父的父亲冲突。因此，我们将 cur 设为 gf，继续循环。
  ⇒

删除

查找

就是普通的二分查找鸭
同理，顺便我们可以给每个遍历过的节点 siz 都 –，因为这些都是新插入节点的父亲
但是这样做有个坑，插入的时候那个节点是不存在的，所以不会给自身siz++，但是删除是会给自身siz++的，后续要避免重复
如果 $cnt > 1$，我们同样只需将 cnt– 就可以返回了

删除

这也和普通平衡树没差多少，为了维持最小的改动，我们尝试找一个子节点来代替它
分情况来讨论：

被删除节点没有孩子或只有一个孩子
这种情况还是简单的，我们只需要用那个孩子（可能是nil）替换被删除节点，注意直接把 cnt，v 复制过去就行了
被删除节点有两个孩子
这种情况下，我们找个离它最近的节点来替换（也就是后缀）。同时我们要把后缀的孩子连到后缀的父亲上（容易证明后缀最多只存在一个孩子）。
什么？你问我为什么不是前缀？我不造啊
因为我们把后缀移走了，从后缀的父亲到被删除节点的孩子siz都不对了（多了cnt了，要减掉）

维护

又是让人头疼的维护环节
来分类讨论吧

后缀是红色
移走了不会影响黑高度，返回
后缀是黑色
移走了会影响后缀的孩子所在一支的黑高度，使其减 1，因此，要想方设法把这一支黑高度加 1
和上面插入一样，下面展示的cur是被移走的后缀所在的子树父节点（也就是黑高度–的子树，但是黑高度是平衡的），起始为后缀的孩子
继续分情况讨论（以左为例）
1. 当前点为黑色，兄弟节点也为黑色，并且兄弟的孩子里面至少有一个红色的节点
  
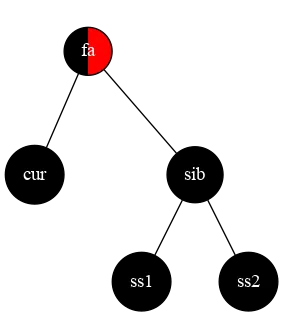
  我们首先将 sib 设为红色，这样两边的黑高度就平衡了，但总体的黑高度还是少 1，如果父亲为黑色，那么我们将 cur 设为 fa 继续循环，如果为红色，将父亲设为黑色就结束啦
2. 当前点为黑色，兄弟节点也为黑色，并且兄弟的孩子都是黑色节点
  
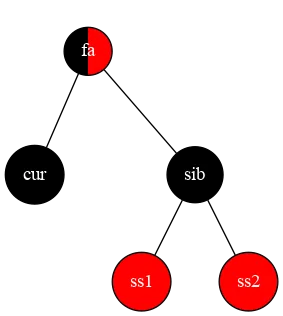
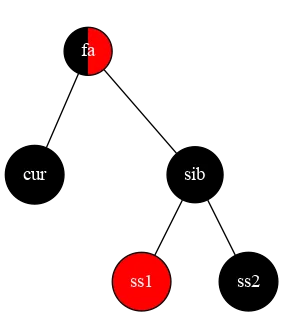
  为了统一，我们将红色的侄子都放到右边
  也就是我们要把第三张图里的树绕 sib 右旋，将 ss1 设为黑色，sib 设为红色， ss2 设为黑色，然后将 sib 设为 s1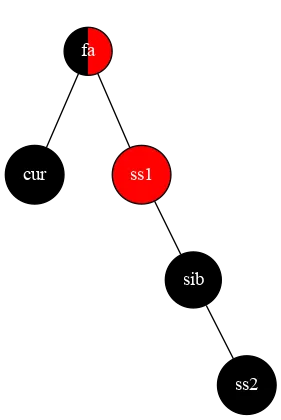
  ⇒
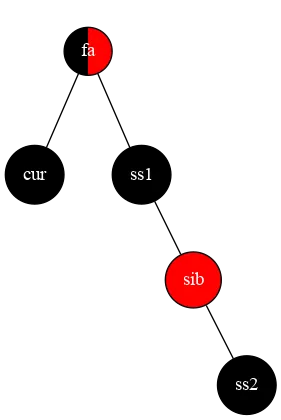
  然后，我们将树绕 fa 左旋，将 ss1 设为 fa 的颜色，fa 设为黑色，sib 设为黑色
  ⇒⇒
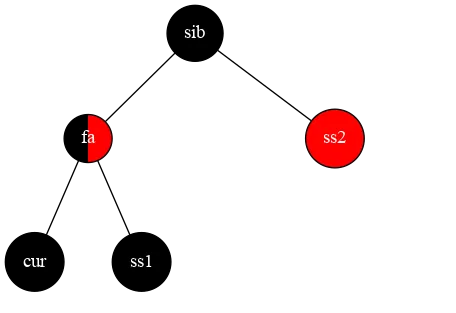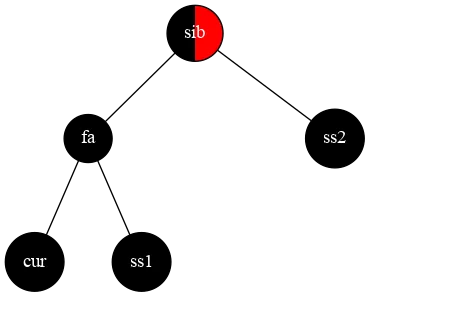
  就结束啦！
3. 当前点为黑色，兄弟节点为红色
  也就是这种情况啦
  
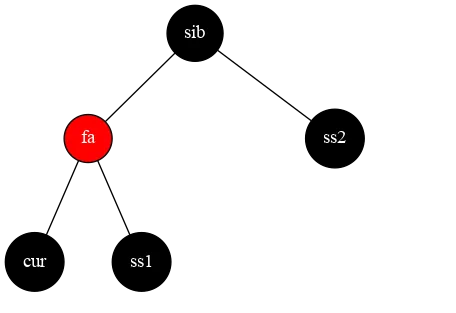
  我们把树绕 fa 左旋，将 fa 设为红色，sib 设为红色，ss2 设为红色，这时就变成其他情形啦，我们继续循环
  ⇒⇒
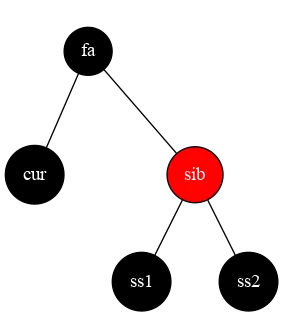4. 当前点为红色
  是最简单的一点啦，只需要将当前点变为黑色，黑高度就正常啦

一点小想法

先设颜色，再旋转
旋转后注意位置的变化，及时修改已有变量

最终代码

// 红黑树代码
#include<iostream>
#define N 1000000
#define fa(x) (rbt[x].fa)
#define siz(x) (rbt[x].siz)
#define cnt(x) (rbt[x].cnt)
#define v(x) (rbt[x].v)
#define color(x) (rbt[x].color)

using namespace std;

struct node{
    bool color; //1 red 0 black
    int ch[2];
    int cnt;
    int fa;
    int siz;
    int v;
};

node rbt[N];

int rt,cnt;
int isch(int s){
    return rbt[fa(s)].ch[1]==s;
}
void update_siz(int cur){
    siz(cur)=siz(rbt[cur].ch[0])+siz(rbt[cur].ch[1])+cnt(cur);
}
void rotate(int cur,bool dir){ // left 0 right 1
    int c1=rbt[cur].ch[!dir]; // 获取 R
    rbt[cur].ch[!dir]=rbt[c1].ch[dir]; // L 的右孩子设为 R 的左孩子 
    if(rbt[c1].ch[dir]) fa(rbt[c1].ch[dir])=cur; // 如果 R 的左孩子存在，则设置父亲为 L
    fa(c1)=fa(cur); // R 的父亲为 L 的父亲
    if(!fa(cur)){ // L 的父亲的孩子设为 R（考虑 L 的父亲为根）
        rt=c1;
    }else{
        rbt[fa(cur)].ch[isch(cur)]=c1;
    }
    rbt[c1].ch[dir]=cur; // R 的左孩子设为 L
    fa(cur)=c1; // L 的父亲设为 R
    update_siz(cur); 
    update_siz(c1);
}
void ins_fix(int cur){
    while(color(fa(cur))){
            int fa=fa(cur),gf=fa(fa);
            bool fa_dir=isch(fa),cur_dir=isch(cur);
            if(color(rbt[gf].ch[!fa_dir])==0){
        		if(fa_dir!=cur_dir){
                	rotate(fa,fa_dir);
                	swap(fa,cur);
        		}
                // if no sibling is ok because the initial value is 0
                color(fa)=0,color(gf)=1;
                rotate(gf,!fa_dir);
                return;
            }else{
                color(fa)=color(rbt[gf].ch[!fa_dir])=0;
                color(gf)=1;
                cur=gf;
            }
    }
    color(rt)=0;

}
void ins(int x){

    int cur=rt,fa=0;
    while(cur){
        siz(cur)++;
        if(x==v(cur)){
            cnt(cur)++;
        	return;
        }
        fa=cur,cur=rbt[cur].ch[x>v(cur)];
    }
    bool cur_dir=x>v(fa);
    if(!rt) rt=++cnt,rbt[cnt]=(node){0,{0},1,0,1,x};
    else rbt[fa].ch[cur_dir]=cur=++cnt,rbt[cnt]=(node){1,{0},1,fa,1,x};
    if(color(fa)==0) return;
    ins_fix(cur);
}


void del_fix(int cur){
    while(cur!=rt){
    	if(color(cur)==1){
    		color(cur)=0;
    		break;
    	}
    	bool dir=isch(cur);
    	int fa=fa(cur),sib=rbt[fa].ch[!dir];
    	if(color(sib)==0&&(color(rbt[sib].ch[0])||color(rbt[sib].ch[1]))){
    		if(color(rbt[sib].ch[dir])==1){
    			color(sib)=1,color(rbt[sib].ch[dir])=0;
            	rotate(sib,!dir);
            	sib=fa(sib);
            }
            color(rbt[sib].ch[!dir])=0;
            color(sib)=color(fa);
            color(fa)=color(rbt[sib].ch[!dir])=0;
            rotate(fa,dir);
            break;
    	}else if(color(sib)==0){
    		color(sib)=1;
    		cur=fa;
    	}else{
    		color(fa)=1,color(sib)=0;
    		rotate(fa,dir);
    	}
    }
    color(rt)=0;
}
void del(int x){
    int cur=rt;
    while(cur){
        siz(cur)--;
        if(x==v(cur)) break;
        cur=rbt[cur].ch[x>v(cur)];
    }
    if(!cur) throw "not exist";
    if(cnt(cur)>1){
        cnt(cur)--;
        return;
    }

    int fcur=cur;
    if(rbt[cur].ch[0]&&rbt[cur].ch[1]){
        fcur=rbt[cur].ch[1];
        while(rbt[fcur].ch[0]) fcur=rbt[fcur].ch[0];
    }
    int scur=rbt[fcur].ch[!rbt[fcur].ch[0]]; // get non-empty child
    if(fcur==rt) rt=scur;
    else rbt[fa(fcur)].ch[isch(fcur)]=scur;
    fa(scur)=fa(fcur);
    v(cur)=v(fcur),cnt(cur)=cnt(fcur); // copy data
    // suffix to root update size
    if(fcur!=cur){
    	for(int cc=fa(fcur);cc!=cur;cc=fa(cc)) siz(cc)-=cnt(fcur);
    }
    // fcur == rt
    if(!color(fcur)){
    	del_fix(scur); //black causes bheight loss
    }
  
}
int kth(int x){
    if(!rt) throw "no root";
    int cur=rt;
    while(cur){
        if(x<=siz(rbt[cur].ch[0])){
            cur=rbt[cur].ch[0];
        }else if(x<=siz(rbt[cur].ch[0])+cnt(cur)){
            return v(cur);
        }else{
        	x-=siz(rbt[cur].ch[0])+cnt(cur);
            cur=rbt[cur].ch[1];
            
        }
    }
    throw "not found";
}
int rnk(int x){
    ins(x);
    int cur=rt,sum=0;
    while(cur){
        if(x<v(cur)){
            cur=rbt[cur].ch[0];
        }else if(x==v(cur)){
        	sum+=siz(rbt[cur].ch[0]);
            break;
        }else{
        	sum+=siz(rbt[cur].ch[0])+cnt(cur);
            cur=rbt[cur].ch[1]; 
        }
    }
    del(x);
    return sum+1;

}
int prefix(int x){
    if(!rt) throw "no root";
    int cur=rt,tar=-0x3F3F3F3F;
    while(cur){
        if(v(cur)>=x){
        	cur=rbt[cur].ch[0];
        }else{
        	tar=v(cur);
        	cur=rbt[cur].ch[1];
        }
    }
    return tar;
}
int suffix(int x){
    if(!rt) throw "no root";
    int cur=rt,tar=0x3F3F3F3F;
    while(cur){
        if(v(cur)<=x){  
        	cur=rbt[cur].ch[1];
        }else{
        	tar=v(cur);
        	cur=rbt[cur].ch[0];
        }
    }
    return tar;
}

int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        static int ac,t1;
        cin>>ac>>t1;
        if(ac==1) ins(t1);
        else if(ac==2) del(t1);
        else if(ac==3) cout<<rnk(t1)<<"\n";
        else if(ac==4) cout<<kth(t1)<<"\n";
        else if(ac==5) cout<<prefix(t1)<<"\n";
        else if(ac==6) cout<<suffix(t1)<<"\n";
    }
}

概念讲解#

红黑树的性质#

旋转#

插入#

查找#

维护#

删除#

查找#

删除#

维护#

一点小想法#

最终代码#

概念讲解

红黑树的性质

旋转

插入

查找

维护

删除

查找

删除

维护

一点小想法

最终代码