无源场:$\nabla = 0$ / 第二类曲面积分为 0
无旋场:第二类曲线积分为 0
静电场:有源无旋场 保守力场
磁场:无源有旋场 非保守力场
感生电场:无源有旋场 非保守力场
基本复习 #
相对论 #
尺缩:$L=L_0\sqrt{1-\frac{u^2}{c^2}}$
钟慢:$t=\frac{t_0}{\sqrt{1-\frac{u^2}{c^2}}}$
质量:$m=\frac{m_0}{\sqrt{1-\frac{u^2}{c^2}}}$
总能量:$E=m'c^2=E_k+E_0$
电场 #
$$F=\frac{q_1q_2}{4\pi\varepsilon_0}\cdot\frac{1}{r^2}$$恒定磁场 #
$$dB=\frac{\mu_0I}{4\pi}\frac{dl\times r_0}{r^2}$$$$B=\frac{\mu_0}{4\pi a}(cos\theta_0-cos\theta_1)$$$$B=\frac{\mu_0IR^2}{2(R^2+x^2)^{3/2}}$$$$B=\frac{\mu_0nI}{2}(cos\theta_1-cos\theta_2)$$$x=0$,$B=\frac{\mu_0 I}{2R} \rightarrow B=\frac{\mu_0I\theta}{4\pi R}$
$x >> R$,$B = \frac{\mu_0IR^2}{2x^3} = \frac{\mu_0IS}{2\pi x^3} = \frac{\mu_0}{2\pi} \frac{p_m}{x^3}$
无限长 $B = \mu_0nI$
电荷激发的磁感应强度 #
$$B=\frac{\mu_0}{4\pi}\frac{q\,v\times r_0}{r^2}$$$$\Phi_m=\oint_SB\,dS$$
穿出为正方向
磁场的高斯定理 #
$$\oint_SBdS=0$$安培环路定理 #
$$\oint_LB\cdot dl=\mu_0\sum_{inner}I_i$$磁场对载流线圈的作用 #
-
$$M=nBISsin\varphi=p_m\times B$$
$\varphi$ 为线圈面法向向量与磁感应强度方向夹角 -
非均匀
运动趋势使线圈所围平面的磁通量增大
磁力的功 #
$$A=I\Delta\Phi_m$$投影面积 $S_0 = Scos\theta$
磁介质 #
分类
- 顺磁质
- 抗磁质
- 铁磁质
电磁感应 #
动生 #
$$\varepsilon=(v\times B)dl$$感生 #
$$\oint_LE\cdot dl = -\frac{d\phi}{dt}=-\int_S\frac{\partial B}{\partial t}dS$$$$\displaylines{\varepsilon_总=\varepsilon_{动生}+\varepsilon_{感生}=\int_L(v\times B)\cdot dl-\int_S\frac{\partial B}{\partial t}dS=-\frac{d\Phi}{dt} \\ q=\int Idt=\frac{1}{R}\int-\frac{d\phi}{dt}\cdot dt=\frac{1}{R}\Delta\phi}$$自感 #
$$\displaylines{N\Phi=LI , N\Phi=NBS=\mu_0\frac{N^2}{l}SI\Rightarrow L=\mu_0\frac{N^2}{l}S\\ \varepsilon_L=-L\frac{dI}{dt}}$$互感 #
$$\displaylines{\Phi_{21}=MI_1 \\ \varepsilon_{21} = -M\frac{dI_1}{dt}}$$
$M = k\sqrt{L_1L_2} (0\leq k \leq 1)$
涡流 #
$$Q \propto \nu^2$$磁场能量 #
$$W_m=\frac{1}{2}LI^2$$$$W_m=\frac{1}{2}\frac{B^2}{\mu}=\frac{1}{2}BH$$麦克斯韦方程组 #
位移电流 #
| 位移电流 | 传导电流 |
|---|---|
| 变化的电场 | 自由电荷的定向运动 |
| 不需要导线 | 需要导线 |
| 不产生焦耳热 | 产生焦耳热 |
| $$\displaylines{\oint_SD\cdot dS = \sum q \\ \oint_SB\cdot dS = 0 \\ \oint_LE\cdot dl=-\int_S\frac{\partial B}{\partial t}\cdot dS \\ \oint_LH\cdot dl = \sum I+\int_S\frac{\partial D}{\partial t}dS}$$ |
气体动理论 #
$$pV=\frac{M}{\mu}RT \Longleftrightarrow p=nkT(k = \frac{N}{V}, k = \frac{R}{N_A})$$$$\displaylines{ p=\frac{1}{3}nm\overline{v^2}=\frac{2}{3}n\overline{\varepsilon_t} \\ \overline{\varepsilon_t}=\frac{3p}{2n}=\frac{3nkT}{2n}=\frac{3}{2}kT(\varepsilon_t 为平均平动动能)}$$方均根: 平方的均值的平方根 $\sqrt{\frac{\sum_{i=1}^nX_i}{n}}$
能量按自由度分配的统计规律 #
| 分子种类 | 平动自由度 | 转动自由度 | 总自由度 |
|---|---|---|---|
| 单原子分子 | 3 | 0 | 3 |
| 刚性双原子分子 | 3 | 2 | 5 |
| 刚性三原子以上分子 | 3 | 3 | 6 |
气体分子数按速率分布的统计规律 #
$$f(v)=4\pi\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-\frac{mv^2}{2kT}}v^2$$
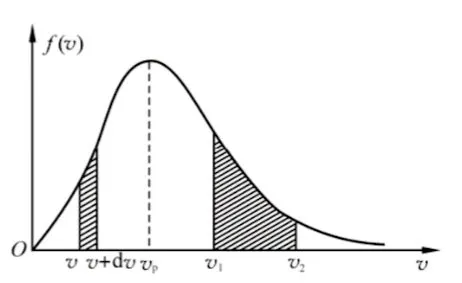
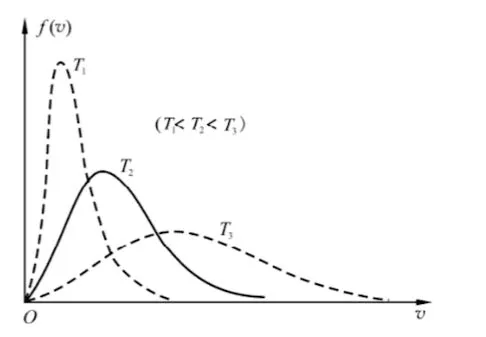
- 平均速率 $\overline{v} = \sqrt{\frac{8kT}{\pi m}} \approx 1.60\sqrt{\frac{Rt}{\mu}}$
- 最概然速率 $v_p=\sqrt{\frac{2kT}{m}} \approx 1.41\sqrt{\frac{Rt}{\mu}}$
- 方均根速率 $v_{rms} = \sqrt{\frac{3kT}{m}} \approx 1.73 \sqrt{\frac{RT}{\mu}}$
气体分子数按能量分布的统计规律 #
$$f=n_0\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-\frac{\varepsilon_p+\varepsilon_k}{kT}}$$$$n=n_0 e^{-\frac{\varepsilon_p}{kT}}$$$$n=n_0e^{-\frac{mgz}{kT}} \xrightarrow{p=nkT} p=n_0e^{-\frac{mgz}{kT}}kT \rightarrow p=p_0e^{-\frac{mgz}{kT}}$$平均碰撞频率和自由程 #
$$\overline{Z}=\sqrt{2}\pi d^2n\overline{v}$$$$\overline{\lambda}=\frac{\overline{v}}{\overline{Z}}=\frac{1}{\sqrt{2}\pi d^2n}$$
d: 分子有效直径
量子力学基础 #
黑体辐射 #
实验规律 #
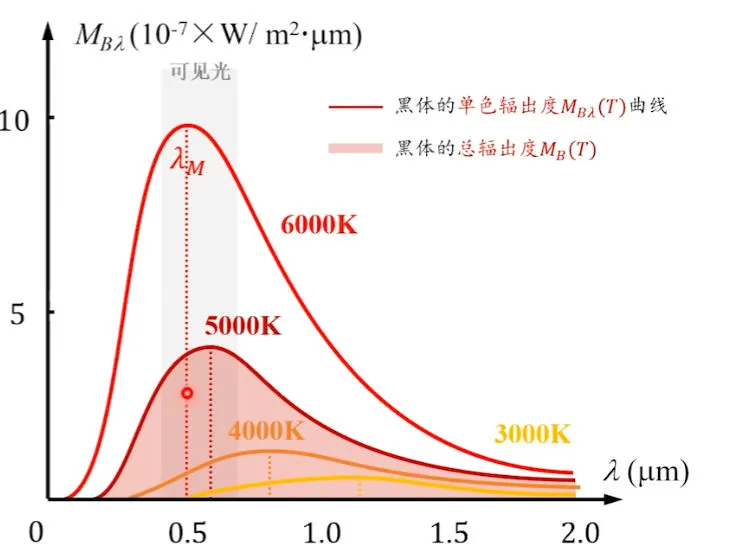
$M_\beta(T)=\sigma T^4$
$T\lambda_M=b$
能量量子化: $\varepsilon=h\nu$
光电效应 #
赫兹首先发现
- 饱和电流$i_S$: $i_S\propto I$
- 遏止电压$U_\alpha$: 仅与光的频率有关 $eU_\alpha=\frac{1}{2}mv_0^2, U_\alpha=K\nu-U_0, \frac{1}{2}mv_{max}^2=e(K\nu-U_0)$
$\Rightarrow h=eK, A=eU_0$
康普顿效应 #
汤姆孙:枣糕
卢瑟福:有核
证明光子理论的正确性(光具有量子性)
说明光子具有质量动量和能量,证明能量守恒和动量守恒适用
例3.3:光电效应和康普顿效应都包含电子与光子的相互作用,仅就光子和电子相互作用而言,下列说法正确的是(${\color{Green}BC}$)
A.两种效应都属于光子和电子的弹性碰撞过程;
B.光电效应是由于金属电子吸收光子而形成光电子,康普顿效应是由光子和自由电子弹性碰撞而形成散射光子和反冲电子;
C.康普顿效应同时遵从动量守恒和能量守恒定律,而光电效应只遵从能量守恒定律;
D.两种效应都遵从动量守恒和能量守恒定律。 \
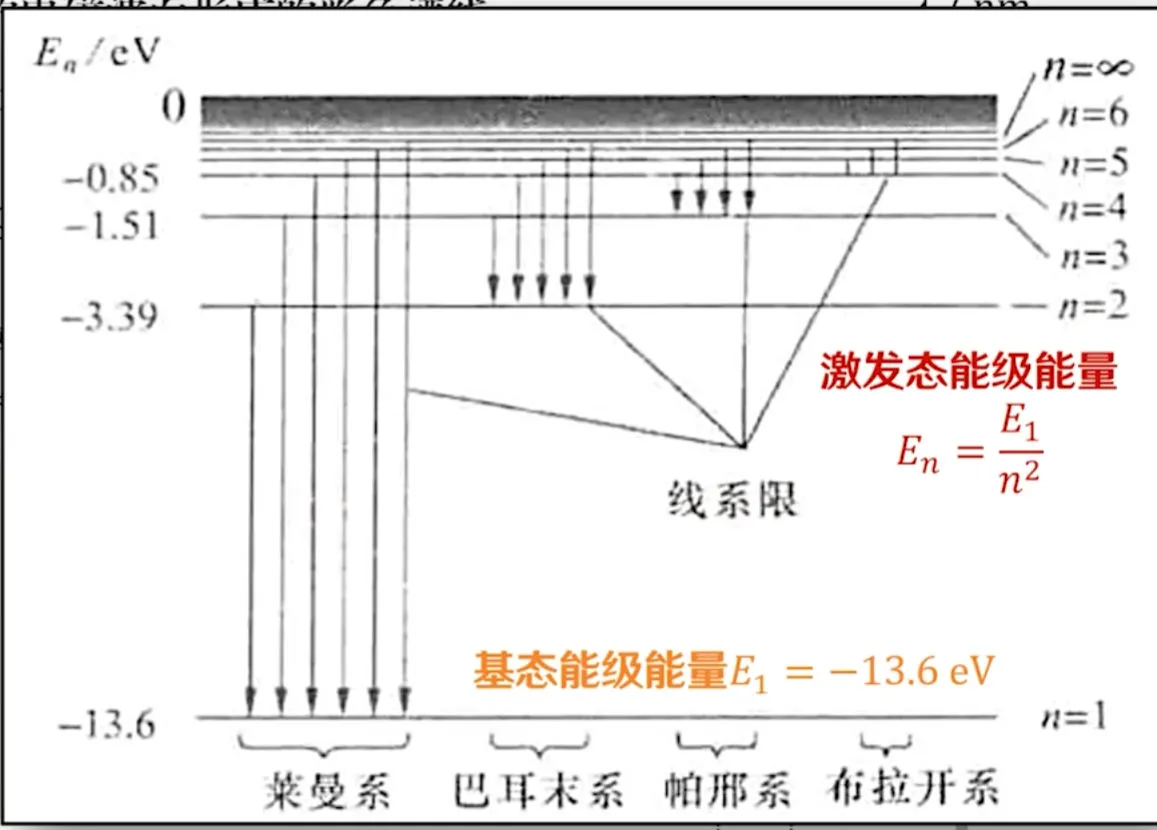
氢原子光谱 #

氢原子理论:
- 定态假设 电子只能处于不连续的特定轨道上
- 量子化条件 电子的角动量只能去特定值的整数倍
- 频率条件 定态越前才能发射光子
波粒二象性 #
$$\displaylines{\varepsilon=h\nu \\p=mc = \frac{h\nu}{c} = h /\lambda}$$海森堡不确定原理 #
$$\Delta x\Delta p_x\geq \frac{\hbar}{2}$$$$\Delta E\Delta t \geq \frac{\hbar}{2}$$
$\Delta p_x=\frac{h}{\lambda-1/2\Delta\lambda}-\frac{h}{\lambda+1/2\Delta\lambda}$
波函数 薛定谔方程 #
$$\Psi(r,t)\Psi_0exp\{-\frac{i}{h}(Er-rp)\}$$
单值,有限且连续
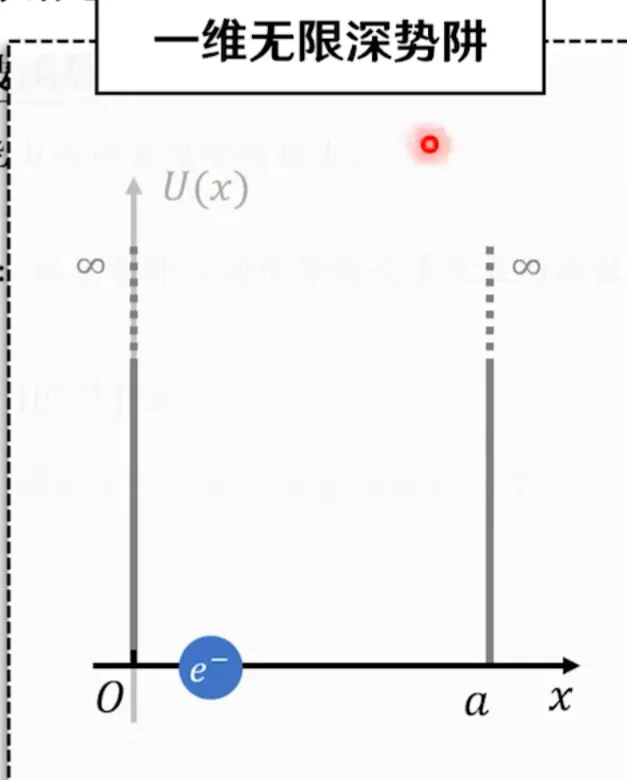
四个量子数 #
斯特恩-盖拉赫实验证实了:原子的自旋磁矩取向量子化 (考试考过)

多原子系统的壳层结构 #
泡利不相容原理:即不可能有两个电子的四个量子数全相同

能量最小原理: 占据能量最小的能级
徐光宪定则:对壳层(n,l),n+0.7l 的值越大,能级能量越高
n 确定时可以容纳 $2n^2$ 个不同的量子态电子